Como explicar o conhecimento por meio da sociologia? Para exemplificar o que propunha, David Bloor arriscou-se a estudar sociologicamente o mais puro, abstrato e inquestionável dos conhecimentos: a matemática. Não uma sociologia dos matemáticos, mas da própria lógica matemática.
Todos aceitam que seria possível haver uma sociologia da matemática relativamente modesta que estudasse o ingresso profissional, a evolução das carreiras e tópicos semelhantes. Isso poderia com justiça ser chamado de sociologia não da matemática, mas dos matemáticos. Questão mais controversa é se a sociologia pode atingir o âmago do conhecimento sociológico. Ela seria capaz de explicar a necessidade lógica de um passo em um argumento, ou por que uma prova é, de fato, uma prova?[1]
A proposta ousada de Bloor é a de mostrar como ocorre a construção do conhecimento matemático por componentes chamados por ele de naturalistas: processos mentais, padrões de comportamento, hábitos, experiências, entre outros. O autor não mede esforços de investigação e de argumentação para penetrar no reino da objetividade, da universalidade e da impessoalidade desse conhecimento, buscando sua causalidade social.

As primeiras incursões ao tema vieram como parte de suas leituras sobre as teorias de Mannheim, Lakatos e Wittgenstein. Foram aglutinadas no artigo de 1973 intitulado Wittgenstein and Mannheim on the Sociology of Mathematics. Para o livro Conhecimento e imaginário social, Bloor dedica extensa análise sobre o assunto, que ocupa três capítulos da obra. Neste texto, apresenta-se um apanhado geral do que é discutido no primeiro deles: Uma abordagem naturalista à matemática.
Para estudar a matemática sob o enfoque da sociologia do conhecimento é preciso, além de reafirmar os princípios do Programa Forte, enfrentar o ponto de vista realista que “concebe as verdades matemáticas como objetos pertencentes a um reino preexistente e totalmente independente do sujeito cognoscente. Para essa perspectiva ontológica, as verdades matemáticas são vistas como pertencentes a um reino da verdade como tal. Bloor considera o realismo em matemática a concepção que se opõe frontalmente aos propósitos da sociologia da ciência em se estabelecer nesse campo. Se o realismo é válido em matemática, o programa forte não pode frutificar em sociologia da ciência”[2].
x ( x + 2 ) + 1 = ( x + 1 ) ²
No início da exposição de sua abordagem, o autor apresenta um teorema de álgebra e discute como é difícil duvidar da verdade elementar contida naqueles símbolos. Por conta disso, a matemática é extremamente persuasiva, imutável e única. “A autoridade de um passo matemático, tal como se apresenta à nossa consciência, é ao menos semelhante à autoridade moral absoluta (…). Um indivíduo diante da matemática vê-se na presença de um corpo de verdades que têm que ser aprendidas. Há uma clara distinção entre o certo e o errado.”[3]
Em sua abordagem naturalista e crítica, Bloor inicia resgatando a perspectiva do psicologismo, que estuda como a matemática é aprendida. “A matemática pode ser vista como um corpo de habilidades, crenças e processos de pensamento aos quais os indivíduos devem ser iniciados”[4]. Um precursor dessa perspectiva, e que na realidade é anterior a ela, é o filósofo e economista britânico John Stuart Mill. Em 1843 ele apresentou suas ideias sobre a matemática no texto Sistema de lógica.
Mill, como todo empirista, vê o conhecimento como derivado de experiências. A matemática, sendo conhecimento, também seria derivada da experiência. O objetivo de Mill em sua Lógica é o de “mostrar que as ciências dedutivas como a geometria e a aritmética são apenas espécies de ciências indutivas tais como a física e a química o são”[5]. Segundo Bloor, a ideia básica de Mill é a de que para o aprendizado da matemática é necessário um estoque de experiências sobre as propriedades e o comportamento dos objetos materiais. Na base dos processos de raciocínio em matemática, por conseguinte, estão padrões de agrupamento dos objetos físicos.
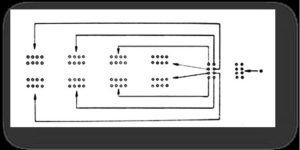
Para entender como as operações matemáticas podem surgir em situações físicas, Bloor utiliza exemplos extraídos do trabalho do matemático, psicólogo e educador Zoltán Pál Dienes. Um deles é o de um jogo que utiliza pedrinhas. “Suponha que dispuséssemos no chão de dez grupos de oito pedrinhas e depois acrescentássemos uma pedrinha. Imagine agora que oito desses grupos permaneçam bem próximos entre si enquanto outros dois formam um par isolado. Podemos agora tomar um dos grupos isolados e utilizá-lo para fornecer uma pedrinha a mais para cada um dos oito grupos. Desse modo, acrescentamos um membro extra a cada um deles. O grupo isolado restante pode então ser acrescido da pedrinha avulsa que foi mencionada antes. Esta rotina de disposição de um dos grupos tem a engenhosa característica reprodutível de terminar somente com grupos que têm o mesmo número de pedrinhas e com um número de grupos que é igual ao número de pedrinhas em cada grupo”[6].
Este é um jogo que representa um exemplo dos muitos que poderiam ser usados com base no mesmo padrão de comportamento e pode ser jogado com um número diversificado de objetos nos grupos e com diferentes números de grupos. Então, Bloor, com base no jogo de Dienes, parte para uma linguagem mais abstrata: “se temos grupos com x pedrinhas em cada um, uma vez que tenhamos dois grupos a mais além do número de pedrinhas em cada grupo, ou seja, (x + 2) grupos, o mesmo padrão de partição e reordenação pode ser executado – não se esquecendo da exigência de prover a pedrinha avulsa. Mediante a separação e da distribuição de um dos grupos entre os demais e da utilização da pedrinha avulsa para cobrir o grupo restante, a mesma reestruturação ocorrerá de novo, o mesmo jogo poderá ser jogado. É claro que, se houver um número errado de pedrinhas, elas não poderão, nesse caso, ser ordenadas e distribuídas do modo engenhoso que a configuração do desenho exibe”[7].
Desenvolvendo essa ideia expressa no jogo de Dienes, chega-se novamente ao teorema já expresso: x (x + 2) x + 1 = (x + 1)². Bloor, analisando esse exemplo, explica em detalhes a conexão das operações com as pedras com o teorema. Na experiência com as pedras, o que se mostra é que a sequência das passagens lógicas da formação do teorema e os seus desdobramentos em outras equações foi produzida enquanto pensava-se e falava-se apenas de coisas, de pedrinhas. No entanto, para Bloor, apesar de promissora, a abordagem de Mill sobre a base empírica do conhecimento matemático precisa ser aprimorada e estendida.
Como forma de mostrar os limites da proposta de Mill, Bloor apresenta as críticas que o matemático Gottlob Frege fez ao empirista em seu Fundamentos da aritmética de 1884. Frege quer resgatar a autonomia do conhecimento matemático e é um representante da visão não-naturalista que Bloor quer superar. Mas a intenção do teórico do Programa Forte é mostrar que “as características da matemática que impressionaram tanto Frege podem ser formuladas de um modo tal que estendam a abordagem naturalista de Mill, em vez de simplesmente obstruí-la”[8].
Em um atento exame dos argumentos de Frege, Bloor concede que “os números não são entidades psicológicas nas mentes das pessoas, mas, de algum modo, são objetos do conhecimento independentes”. Todavia, o autor assegura que isso não compromete necessariamente a posição de Mill, pois “sua teoria comporta um componente objetivo uma vez que a aritmética versa sobre propriedades gerais de objetos, como as pedrinhas tão desprezadas por Frege”. Neste caso, porém, Frege tem outra alegação que parece não oferecer saída para a concepção de Mill: “O argumento central aqui é que o numero não pode ser uma propriedade das coisas, uma vez que o modo como as coisas são numeradas depende de como nós a consideramos”[9]. Isto, na opinião de Frege, é o que diferencia o número daquilo que normalmente consideramos ser as propriedades das coisas.
Portanto, para Frege, os números são objetos da razão ou conceitos, possuindo a mais importante das propriedades: objetividade. Bloor destaca como Frege concebe a ideia de objetividade:
Distingo o que chamo de objetivo daquilo que pode ser manuseável, espacial ou efetivo. O eixo da Terra é objetivo, assim como o centro de massa do sistema solar, mas eu não diria que eles são efetivos do modo como a própria Terra o é. Geralmente falamos da Linha do Equador como uma linha imaginária, mas (…) ela não é criação do pensamento, o produto de um processo psicológico: ela apenas é reconhecida ou apreendida pelo pensamento. Se ser reconhecida fosse o mesmo que ser criada, então não poderíamos dizer nada de positivo sobre a Linha do Equador anteriormente à data de sua alegada criação[10].
Bloor aceita a definição de Frege sobre a objetividade, mas, antes de adotá-la, se propõe a investigar o que essa objetividade é. O teórico do Programa Forte analisa os exemplos citados por Frege: “A linha do Equador assemelha-se a um limite territorial, que pode também ser chamado de linhas imaginárias. E pode ser especificado quando dizemos: imagine uma linha que se estenda para o sul ao longo do rio e, em seguida, contorne a borda da floresta pelo leste. Admite-se geralmente que limites territoriais têm o status de convenções sociais, embora isso não queira dizer que sejam “meras” ou “arbitrárias” convenções. Na verdade, eles são de grande importância, uma vez que se relacionam de diversos e complexos modos com a ordem e a regularidade das vidas vividas em seu interior. Além disso, eles não podem ser mudados por capricho ou extravagância. Não se alteram apenas por termos pensado neles – um indivíduo pode ter ideias corretas ou erradas sobre eles e, caso ocorra de ninguém acalentar ima imagem mental, não desaparecem. Eles também não objetos físicos que podem ser manuseados ou percebidos, embora objetos efetivos possam ser usados como seus indicadores ou seus sinais visuais. Por fim, tais limites podem ser referidos em enunciados sobre eventos que ocorreram antes mesmo que qualquer um pensasse neles”[11].
Para Bloor, esse exemplo sugere que coisas com o status de instituição social estejam, talvez, intimamente relacionadas com a objetividade. Seguindo no argumento, o autor também destaca, lançando uma hipótese, que o terceiro aspecto entre o físico e o psicológico é o social. Então, Bloor discorre sobre os outros exemplos apontados por Frege, mostrando como a objetividade pode ser entendida como uma convenção social. Sobre a concepção do centro do cosmo no mundo medieval, o autor acrescenta:
O centro do cosmo também não era um objeto efetivo, no sentido de que as pessoas poderiam esperar vê-lo ou tocá-lo. Ela era objetivo no sentido de Frege. (…) era um conceito teórico, parte de uma teoria cosmológica então adotada. (…) era um fenômeno social, uma crença institucionalizada, parte de uma cultura. Era a imagem de mundo herdada e transmitida, sancionada pelas autoridades, mantida pela teologia e pela moralidade; e retribuía o serviço sustentando-as[12].
Utilizando as ideias que Frege formulou para defender a autonomia e o caráter puro da matemática, Bloor vê uma brecha que permite uma interpretação sociológica: a definição de objetividade. Portanto, Bloor adiciona essa contribuição e outras críticas de Frege a Mill para respaldar de outra forma o seu raciocínio sobre a natureza social da matemática. Ele a usa como um complemento a uma lacuna deixada por Mill: o que dá a matemática o status de matemática; a aura de autoridade; a convencionalidade, tipicidade e tudo aquilo que concede a ela certos padrões que lhe são característicos.
Na visão de Bloor, a leitura social da definição de objetividade de Frege oferece uma pista sobre como Mill também caminhou para essa descoberta, mas de modo involuntário e inconsciente:
Considere o que está envolvido ao falarmos dos modos “característicos” de ordenar, separar e dispor os objetos. Sugerem-se conotações de padrões típicos, usuais ou mesmo tradicionais. Algumas pessoas são capazes de identificar, com base nos padrões característicos trançados num tapete, a região do mundo da qual este provém. Os padrões ou desenhos característicos são quase sempre entidades antes sociais que individuais. O que Mill involuntariamente fez, portanto, foi transmitir a ideia de que nem todas as possíveis disposições, ou procedimentos de ordenar e separar os objetos são relevantes para atuar como experiências paradigmáticas de matemática. De todos os incontáveis jogos que podem ser jogados com pedrinhas, apenas alguns dos padrões que podem ser com eles estabelecidos alcançam o status especial de tornarem-se “modos característicos” de ordená-los e separá-los. Exatamente do mesmo modo, os incontáveis padrões capazes de ser trançados num tapete não são todos igualmente importantes para um grupo de tecelões tradicionais. Há normas para os que virão a tecer os tapetes do mesmo modo como há normas para os que virão a aprender matemática. Com efeito, as considerações que ajudam a estabelecer um dos grupos não podem ser muito diferentes das que estão em operação no outro. Ambos recorrem a um senso inato de ordem e simetria, de repetição agradável, da possibilidade de traços e remates límpidos, de transições e conexões suaves[13].
Com a introdução da ideia de objetividade de Frege à teoria de Mill, Bloor vê uma direção estabelecida para analisar sociologicamente a matemática. Nesse sentido, o teórico do Programa Forte pode traçar uma semelhança entre autoridade lógica e autoridade moral. O componente psicológico proporcionou o conteúdo das ieias matemáticas; o componente sociológico ocupou-se da seleção dos modelos físicos e tornou compreensível sua aura de autoridade
Referências
[1] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p. 131.
[2] GOMES, Vicente de Paula. Causalidade e hermenêutica em Sociologia da Ciência. Campinas: UNICAMP, 2008. p.78. (Doutorado)
[3] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.133.
[4] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.135.
[5] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.136.
[6] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.139.
[7] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.140.
[8] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.135.
[9] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.147.
[10] FREGE apud BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.148.
[11] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.149.
[12] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.151.
[13] BLOOR, David. Conhecimento e imaginário social. São Paulo: UNESP, 2009. p.153.
Cientista social que especula sobre a natureza social das ideias, sobre a não-identidade entre sujeito e objeto na produção do conhecimento e sobre o sentido de se dizer que a vida tem sentido.
